ベクトルの表し方
ベクトルとは大きさと方向を持つ量を表します

ベクトルとスカラーの違い
量を表す方法は
方向を持たないスカラー法と
方向をもつベクトル法があります
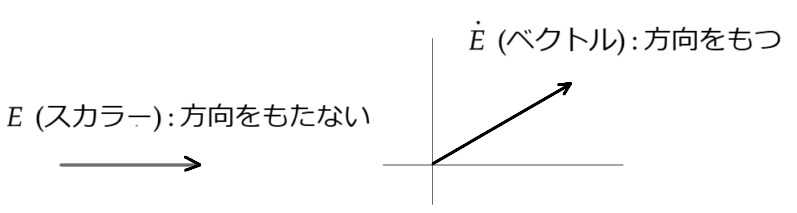
ベクトルを表す式
ベクトルを表す式はx軸とy軸を分けて表記します
x軸は実数(-1、0、0.2、1等)
y軸は虚数(-j1、j0.2、j1等)で表記します
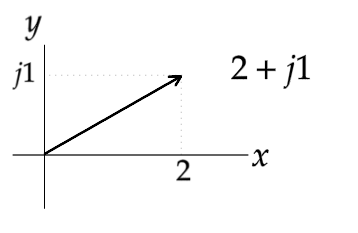
x軸が2、y軸がj1のベクトルは
2+j1 と表記します
ベクトルの大きさは三平方の定理で計算します

ベクトルの合成方法




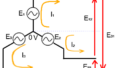
Y結線の線間電圧計算
Y結線の線電流は相電流と同じですが
線間電圧は相電圧の合成となります
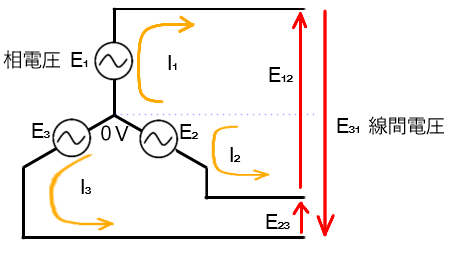
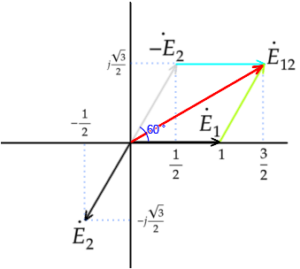
E₁₂はE₁とE₂の合成ですが
E₂は進行方向が逆になるので
-E₂となります
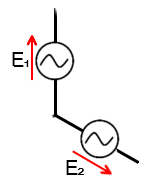
E₁を基準(1)とし、ベクトルを表します
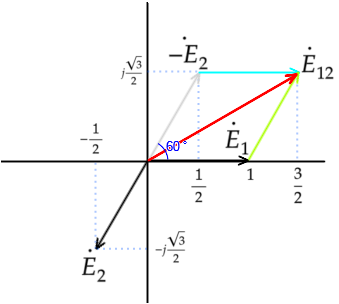
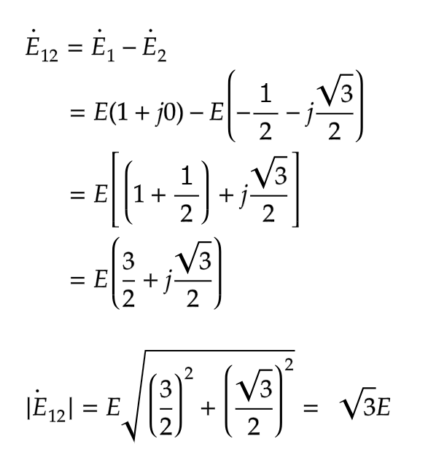
※|X|はXベクトルのスカラー変換です
それぞれの実数部と虚数部を分けて計算します
E₂₃もE₁₂と同様にE₁を基準とした
ベクトルを表します
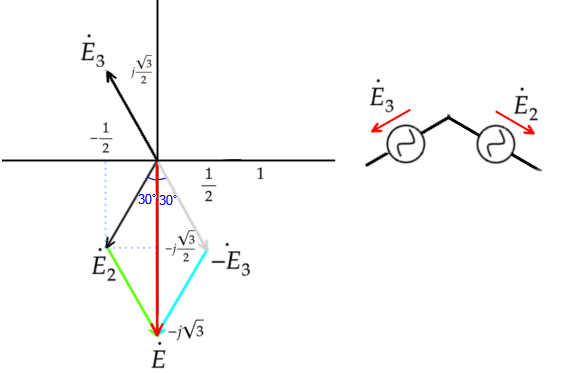
それぞれの実数部と虚数部を分けて計算します
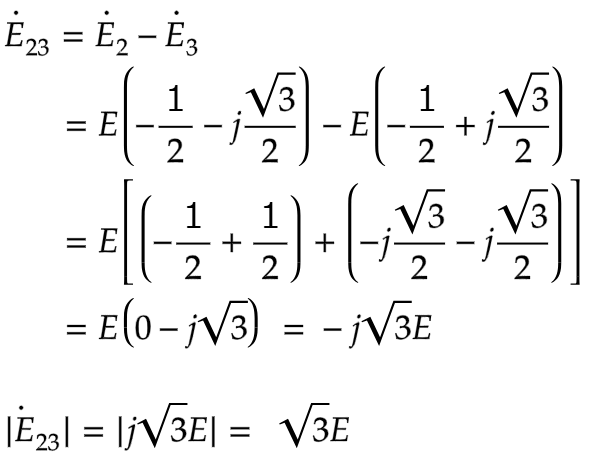
E₃₁もE₁₂と同様にE₁を基準とした
ベクトルを表します
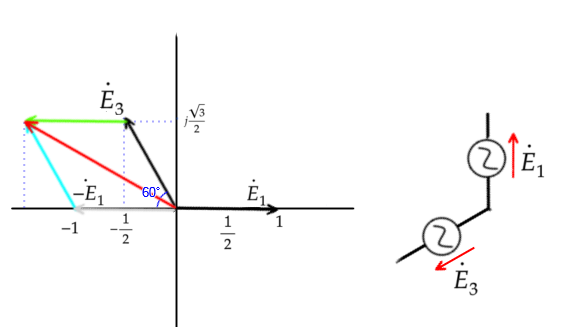
それぞれの実数部と虚数部を分けて計算します
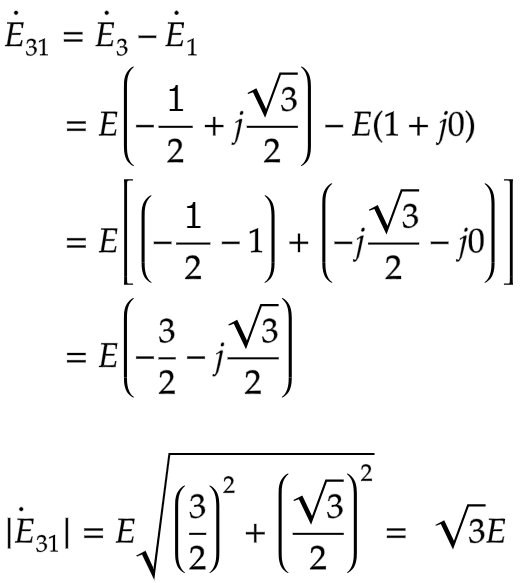

Δ結線の線電流計算
Δ結線の線間電圧は相電圧と同じですが
線電流は相電流の合成となります
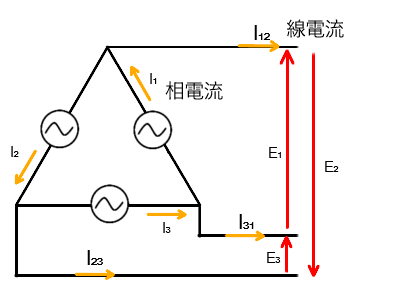
I₁を基準(1)とし、ベクトルを表します
I₁₂はI₁とI₂の合成ですが
I₂は進行方向が逆になるので
-I₂となります
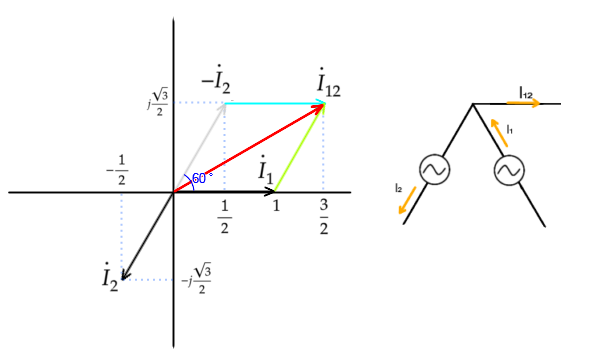
それぞれの実数部と虚数部を分けて計算します
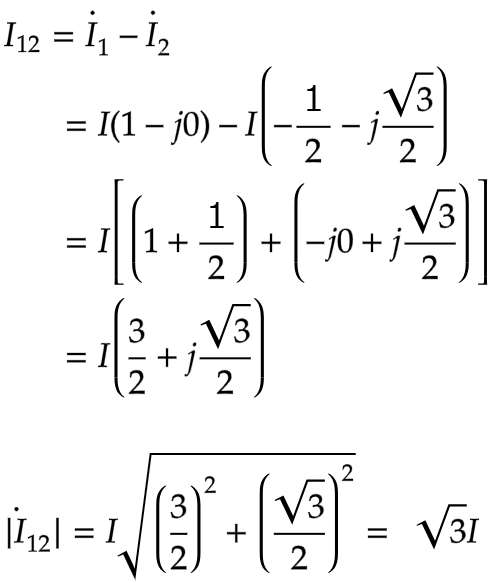
I₂₃もI₁₂と同様にI₁を基準とした
ベクトルを表します
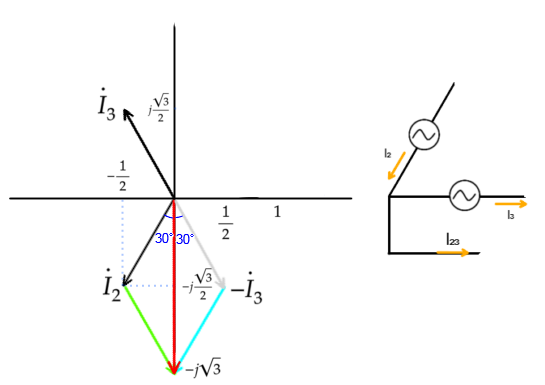
それぞれの実数部と虚数部を分けて計算します
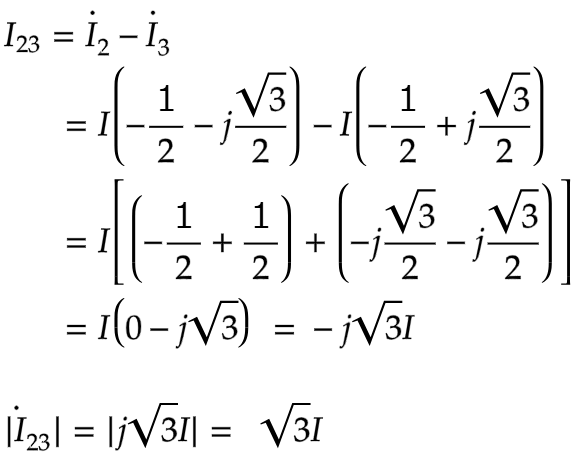
I₃₁もI₁₂と同様にI₁を基準とした
ベクトルを表します
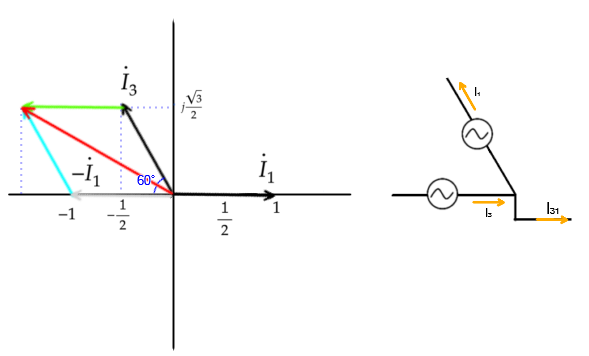
それぞれの実数部と虚数部を分けて計算します
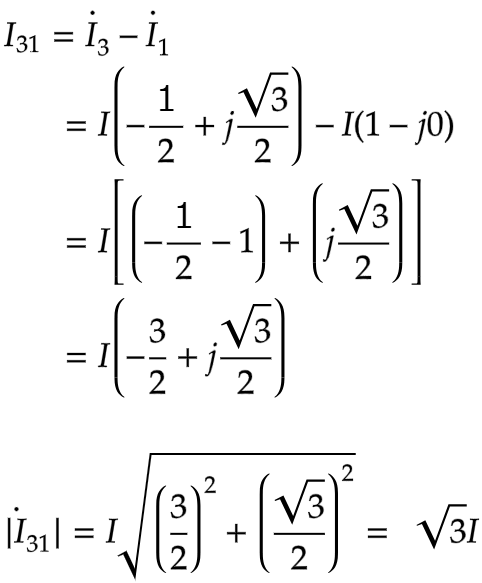



コメント