- 平行導体に働く力
- コイルに働くトルク
- 磁気回路のオームの法則と自己インダクタンス
- 異なる磁性体をもった磁気回路に流れる磁束
平行導体に働く力
問題①
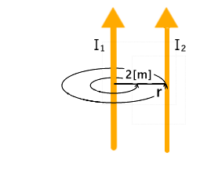
図のような平行導体に働く力と向きを答えよ
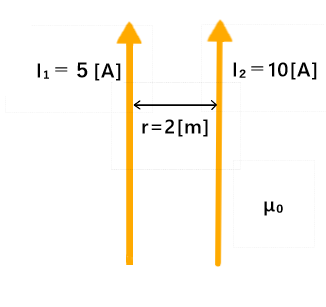
解答
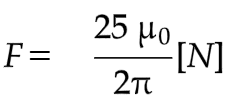
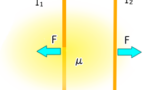
吸引方向に働く
解説
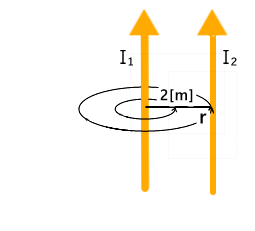

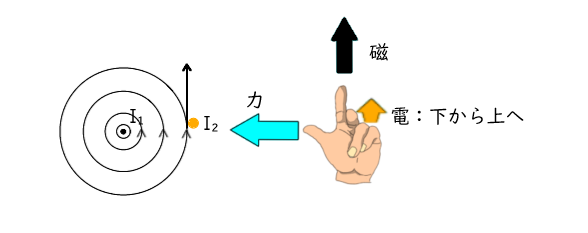
I₂に働く力は、ファラデーの法則により左向きになり、
同様の理由でI₁に働く力はI₂の磁界により右向きとなる。
よって吸引方向に力が働くことになる。
コイルに働くトルク
問題②
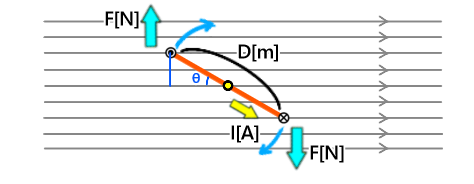
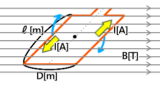
図のコイルに働くトルク[N・m]を求めよ
I=2[A]、ℓ=10㎝、D=20㎝、B=0.5[T]、θ=60°とする
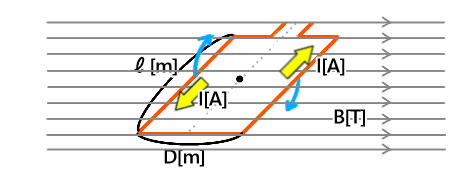
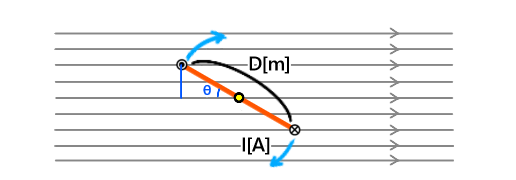
解答
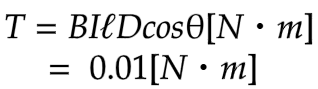
解説
まずは、導線ℓにかかる力 F[N]を求めます
電磁力の公式により、F=BIℓ[N]となります
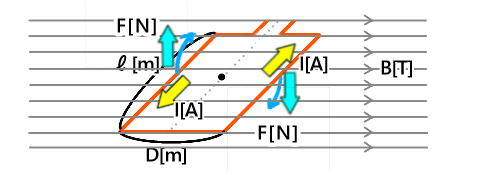
次に、T=FDcosθ[Nm]によりトルクを求めます
T = FDcosθ = BIℓDcosθ[Nm]
I=2[A]、ℓ=10㎝、D=20㎝、B=0.5[T]、θ=60°
T=0.5×2×0.2×0.1×0.5=0.01[Nm] となります。

磁気回路のオームの法則と自己インダクタンス
問題①
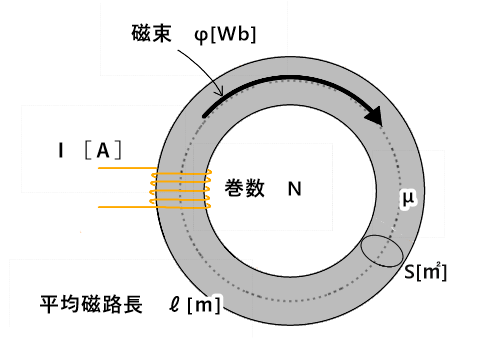
図の磁気回路の透磁率μ[H/ⅿ]と自己インダクタンスL[H]求めよ
I=10[A]、ℓ=20[cm]、φ=0.5[Wb]、S=1[㎡]、N=10巻
解答
μ=1×10⁻³[H/ⅿ] 、L=0.5[H]
解説
透磁率が関係するのは磁気抵抗Rmであることに注目します
Rmは、NIとφにより求められます

次にRmの公式より透磁率μを求めることができます

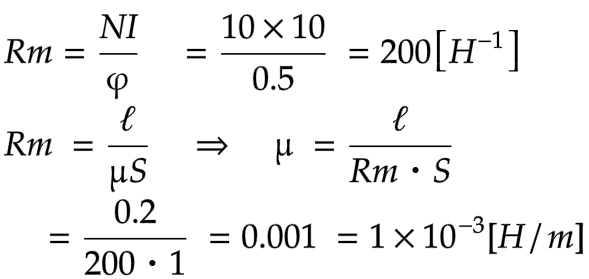
自己インダクタンスL[H]は、NI=Lφの公式により求めます
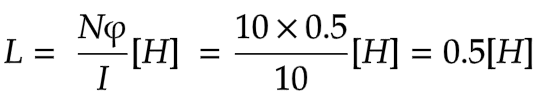
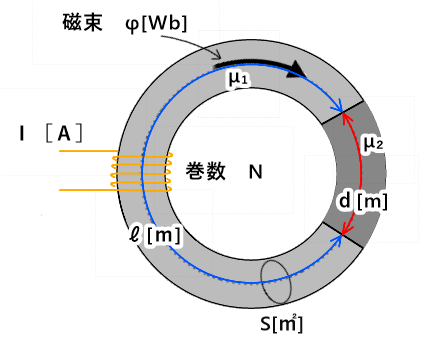
異なる磁性体をもった磁気回路に流れる磁束
問題
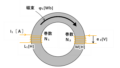
図のような透磁率μ₁ ℓ[m]と、μ₂ d[m]の磁性体
を合成した時に流れる磁束を求めよ
I=2[A]、N=5巻き、ℓ=0.7[m]、d=0.3[m]
S=1㎡、μ₁=0.2[H/m]、μ₂=0.5[H/m]
解答
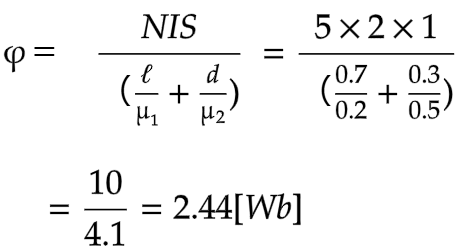
解説
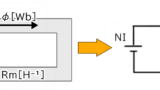
磁気抵抗Rmの公式により
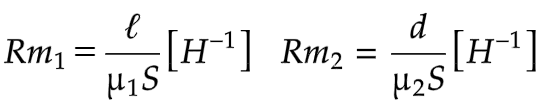
電気回路で表すと下図のようになります
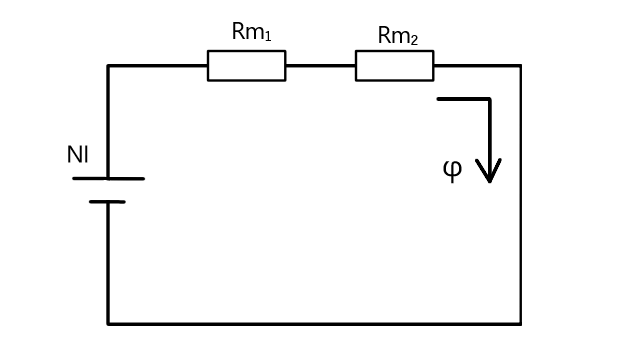
よって、
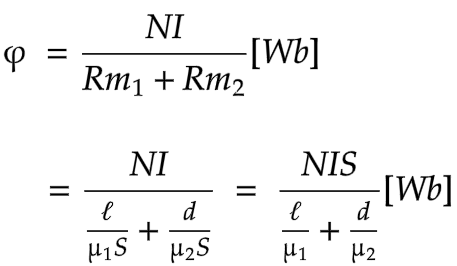
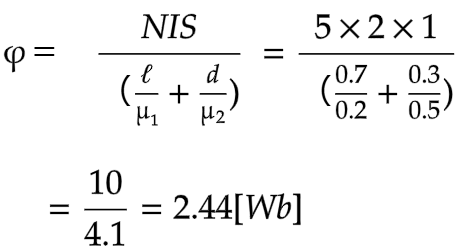



コメント