電界とは?
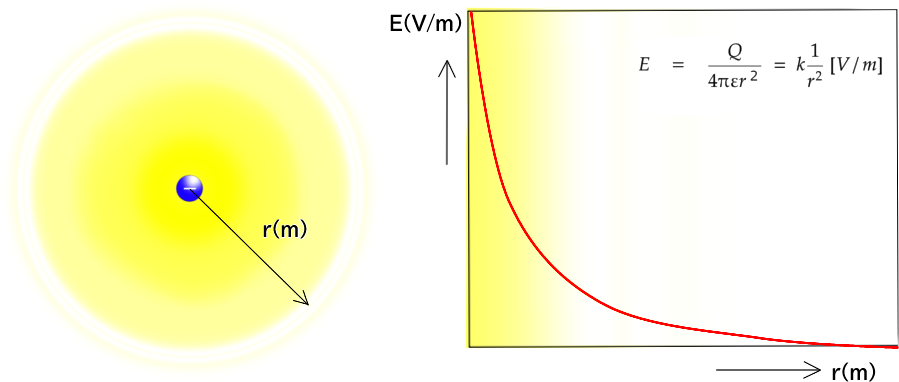
電界の強さとは、電荷のエネルギーが周囲に拡散したものです。磁石から出る磁力のように、周りに見えない力の場ができて、他の電荷に力を及ぼします。 中心から距離が離れると距離の2乗に反比例して電界の力が弱くなります。
電位とは?
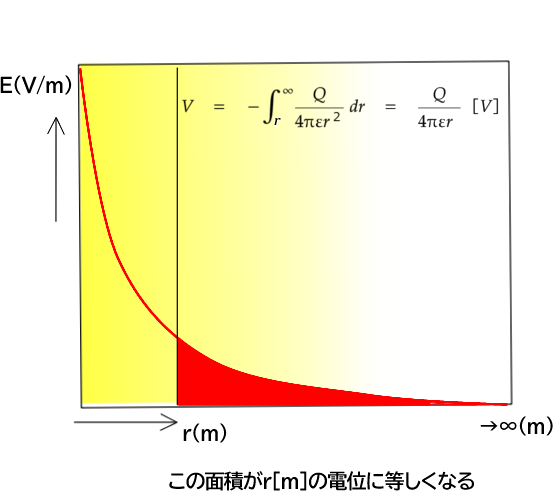
中心~r[m]のところから無限大∞[m]までの電界の強さを積分すると電位[V]となります。電位は中心からの距離に反比例します。
電位差(電圧)とは?
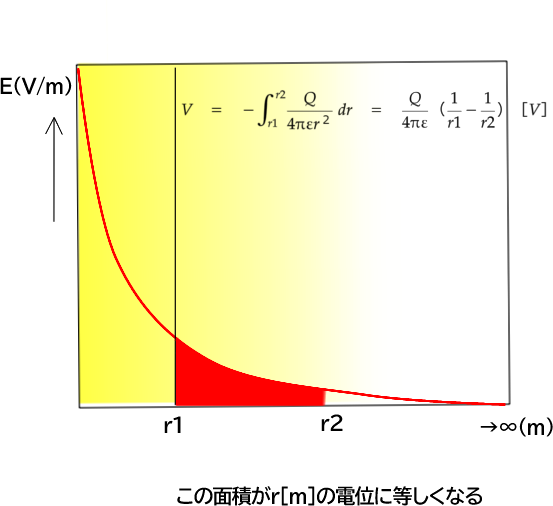
r1[ⅿ]~r2[m]間の電界の強さを積分すると、r1~r2間の電位差[V]となります。 積分値は、赤色の面積になります。

平行版コンデンサーの電界と電圧の関係
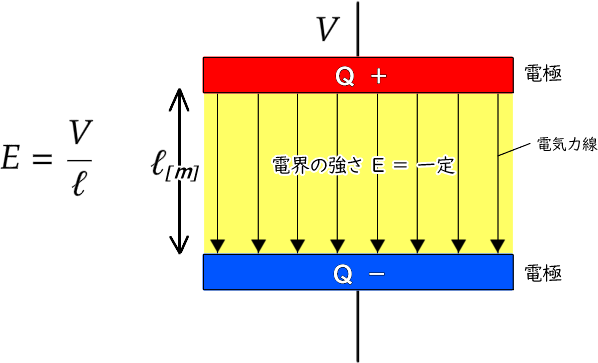
平行板コンデンサーの電極面から均一な密度で電気力線がでます。電気力線の密度が均一なので電界の強さも均一になり、E=V/ℓ となります。
例題①
間隔が2×10₋8ⅿの平行板コンデンサーに5Vの電圧をかけたときに、平行板間の電界の強さは?
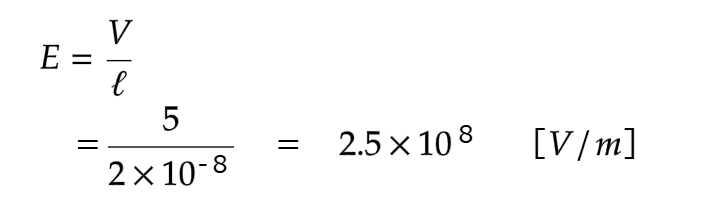
例題②
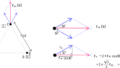
図のように10[m]離れた位置に電荷A,Bがある。 Aからx[m]離れた位置の電界の力E[V/m]を求めよ。 なお、周囲は真空であり誘電率はε₀っとする。
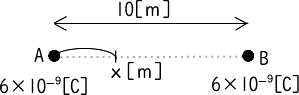
x[m]の合成電界を求めるには、それぞれの電荷の電界を求め、電界の向きに応じて差し引きをする。
まずは、電界Aを求め 次に電界Bを求める。
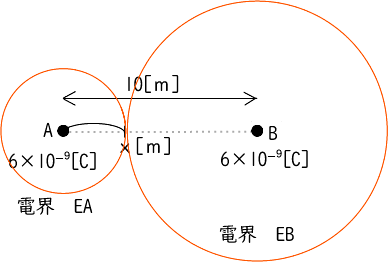
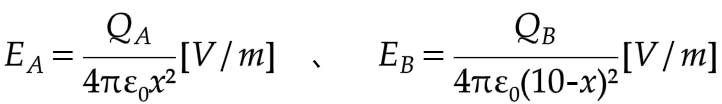
次に、電気力線の方向により電界の向きがきまり、向きが同じなら足し、逆なら引くことで合成電界を求める





コメント