三角関数の基礎　sinカーブ（正弦波）とcosカーブ（余弦波)と回転運動の関係

• sin（正弦）とは？
• sinカーブ（正弦波）と回転運動の関係
• cos（余弦）とは？
• cosカーブ（余弦波）と回転運動の関係

sin（正弦）とは？

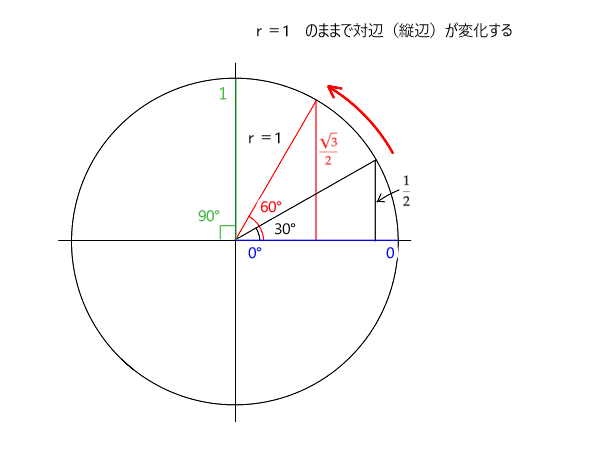
sin（正弦）とは、半径（ｒ）が１の円を回転したときの対辺の長さです。

　　0°⇒０　30°⇒1/2　60°⇒１/√３　90°⇒１　となります。

スポンサーリンク

sinカーブ（正弦波）と回転運動の関係

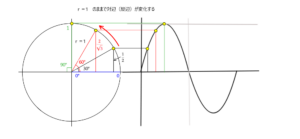
対辺の長さだけをグラフにするとsinカーブ（正弦波）になります。

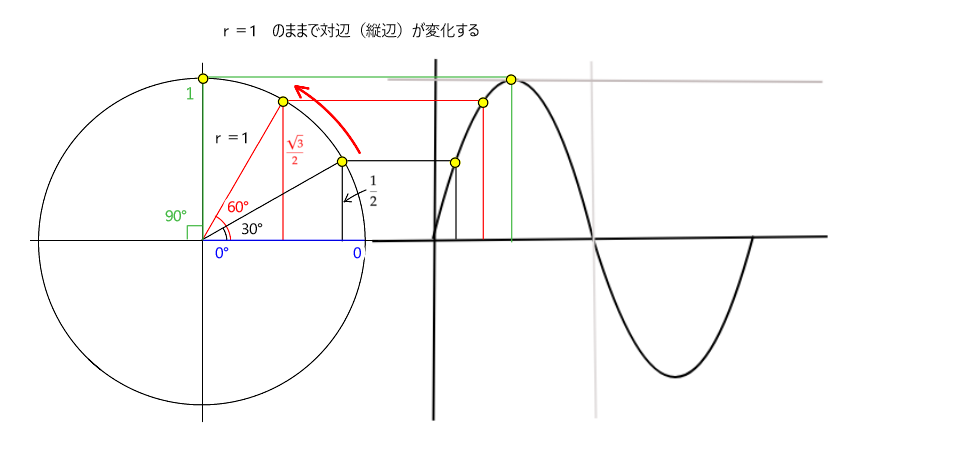
sinカーブは、０°の時に0、90°の時に1　になることを覚えておきましょう。

三角関数換算表　sinθ

cos（余弦）とは

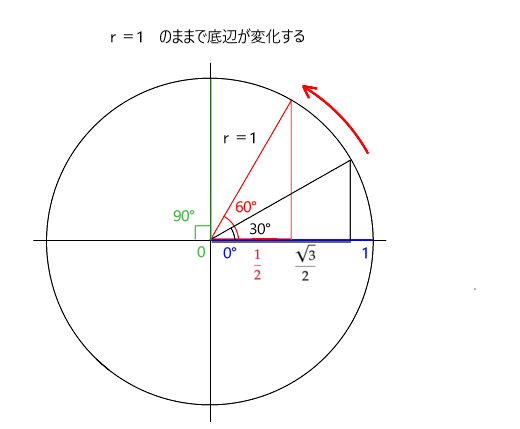
cos（余弦）とは、半径（ｒ）が１の円を回転したときの底辺の長さです。

　　cos0°⇒１　cos30°⇒√３/2　cos60°⇒１/２　cos90°⇒０　となります。

cosカーブ（余弦波）と回転運動の関係

　　底辺の長さだけをグラフにするとcosカーブ（余弦波）になります。

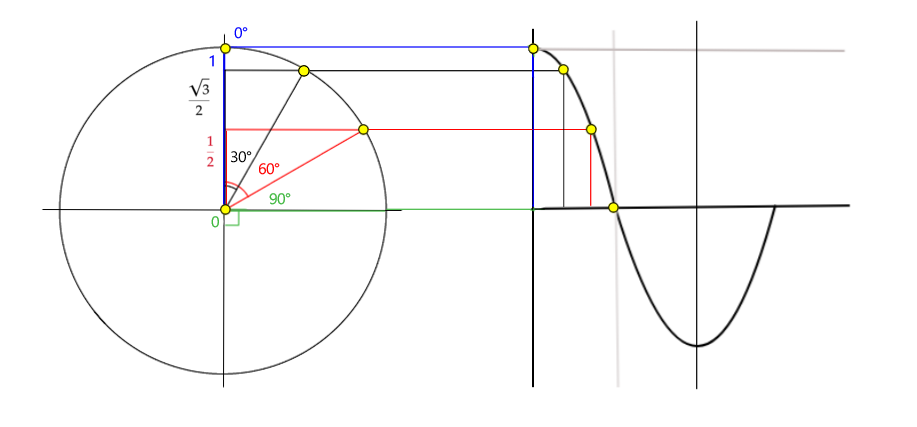
cosカーブは、０°の時に１、90°の時に0　になることを覚えておきましょう

三角関数換算表　cosθ

三角関数sin、cos、tan｜電気を極める – 電気を極める