- クーロンの法則問題① 正三角形の頂点上における3つの電荷に働く力
- クーロンの法則② 水平線上に配置した3つの電荷に働く力
問題①
真空中において、正三角形の各頂点に正電荷を置いたときに電荷QCに働く力F[N]と向きを求めよ
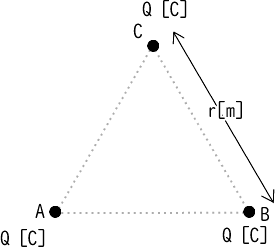
解説
電荷Cが、電荷A,Bから受けるそれぞれの力をベクトルで記し、合成することで解を求めます。
①電荷Aに対して働く反発力(斥力)を求め図に書き込む
②電荷Bに対して同様に図に書き込む
③それぞれのベクトルを合成し力の大きさと方向を示す
① 電荷Aに対して働く反発力(斥力)を求め図に書き込む
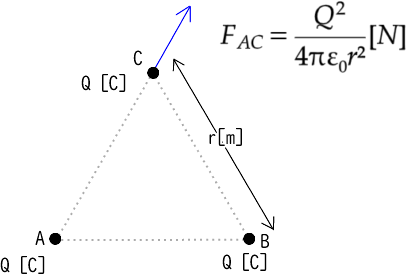
② 電荷Bに対して働く反発力(斥力)を求め図に書き込む
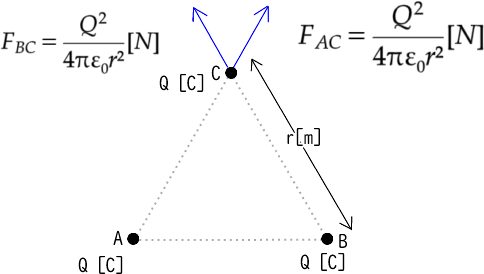
③それぞれのベクトルを合成し力の大きさと方向を示す
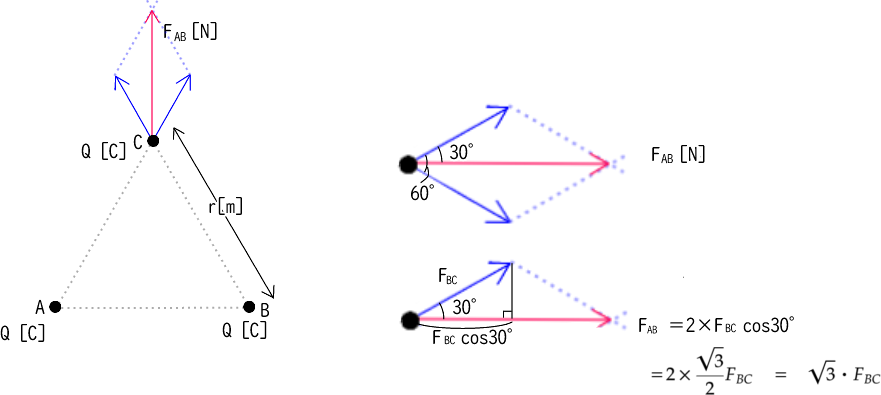
問題②
図のように真空中の直線上に同じ間隔r[m]をおいて、Qa,Qb,Qcの電荷を置く。これらの電荷に働く値からがすべて0となるQb[C]、Qc[C]を求めよ。
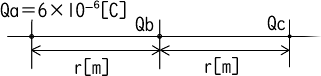
解説
QbにはQaとQcの力が均一に掛かり距離も同じなので、Qc[C]が容易に導ける。Qcがわかれば、Fac=FabよりQb[C]を求めることができる
①Qbに働く力Fab[N]=Fcb[N]である事より、Qc[C]を求める
②Qaに働くFab[N]=Fac[N]になるQb[C]を求める
①Qbに働く力Fab[N]=Fcb[N]である事より、Qc[C]を求める

Fab=Fbc より Qa=Qc ということがわかる。
よって、 Qa= Qc= 6×10⁻⁶[C] となる
②Qaに働くFabーFac=0の時のQb[C]を求める
Fab,Facをそれぞれ求める Facは距離が2倍なので注意する
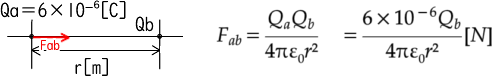
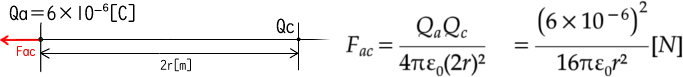
Fac = Fab よりQbを求める
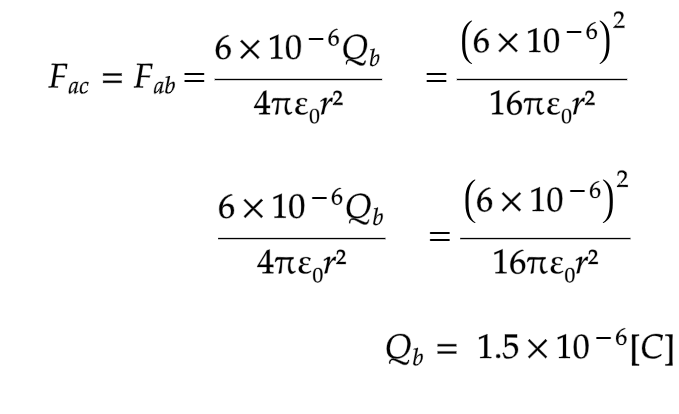
Qbは符号が逆なので、 -1.5×10⁻⁶[C]となる





コメント